다음 코스도 바로 시작했다. 제목으로 내용을 유추해보자면, 저번 코스에서 대략 머신 러닝, 딥 러닝 모델이 어떤 방식으로 작동하는지 파악했으니 이번엔 그 모델을 더 잘 작동할 수 있도록 만드는 방법을 익히는 것이 목표인 것 같다.
우선, 데이터를 나누는 방법부터 시작한다. 아무리 내가 머신 러닝 무식자라지만, 데이터를 학습용, 검증용, 테스트용으로 나누는 것 정도는 알고 있었다. 이 강의에서는 검증용을 개발용이라는 용어로 사용한다. 빅데이터 시대가 되면서 데이터 양이 폭발적으로 증가했기 때문에, 원래 60/20/20 정도로 나누던 비율이 극단적으로 99.5/0.4/0.1 이렇게 바뀌어도 괜찮다는 사실을 새로 알게 됐다. 테스트용이 고작 0.1%라도 10000개 정도 되면 모델을 테스트하기에는 충분하다는 것 같았다.

그리고 개발용 데이터와 테스트용 데이터의 분포에 대해서도 생각할 기회가 있었다. 모델 학습을 개발용 데이터에 대한 성능이 좋도록 진행하는 경우엔 테스트용 데이터와 분포를 맞춰야 한다고 설명한다. 컴퓨터 비전 같은 분야에서는 어떤 카메라로 사진을 찍었냐에 따라서 해상도가 다르고 좋은 해상도로 개발하고 낮은 해상도로 테스트하는 경우엔 당연히 원하는 성능이 안 나올 것이다. 아니면 아싸리 테스트는 생략하는 방법도 있다. 테스트를 하는 이유가 편향되지 않은 데이터에 대해 성능이 얼마나 나오는지를 점검하는 건데, 경우에 따라서는 굳이 하지 않아도 되는 상황도 있을 수 있다고 언급됐다.
그다음은 편차, 분산에 관한 내용이다. 머신 러닝 분야에서 뭐가 편차고 뭐가 분산인지 짚고 갈 수 있어서 좋았다. 대충 강의에서 설명한 내용을 토대로 편차, 분산이 높은 경우를 그려봤는데, 둘 다 높은 경우엔 거의 선형이다가 갑자기 유연한 부분이 생긴다. 편차가 큰 경우엔 Underfitting, 분산이 큰 경우엔 Overfitting 되었다고 한다.

이제 편차, 분산이 높으면 어떤 일이 발생하는지 알았으니까, 결과를 토대로 얼마나 높은지에 대해 점검해야 한다. 보통 Train Set의 오차와 Dev Set의 오차를 활용한다. Train Set의 오차를 보고 편차를, Train Set과 Dev Set의 차이를 보고 분산을 결정한다. 밑의 표처럼 오차가 어느 정도 나왔느냐에 따라서 어떤 문제가 있는지 파악할 수 있다.

문제를 알았으니, 이제는 해결만 하면 된다. Basic recipe for machine learning라는 플로우 차트를 통해서 문제를 해결한다. 각각에 문제에 맞는 방법을 써야 결과가 개선된다. Bias가 크다고 데이터를 더 수집해봤자 결과가 크게 달라지지 않는다. 그리고 예전에 비해 요새 문제 해결 기술이 많이 발전해서 Bias-Variance trade-off가 많이 감소했다고 한다. 이번 학기 수업을 들으면서 Bias-Variance 배울 때는 trade-off가 꽤나 있다고 했었는데, 어떤 분야에서 어떤 방법을 적용하느냐에 따라 달라지나 보다.

Bias가 큰 경우엔 문제 해결 방법이 꽤나 명확하다. 하지만 Variance의 경우에는 데이터를 추가적으로 수집하는 데에는 시간과 돈이 많이 들기 때문에 많은 데이터를 확보한다는 것은 현실적으로 어려울 수 있다. 그래서 정규화라는 방법을 많이 사용한다. Regularization에는 L2랑 L1이 있다. 우선 Logistic 회귀에서 정규화가 어떻게 쓰이는지 살펴보자. 가중치가 커질수록 페널티가 커지기 때문에 정규화를 도입하면 가중치가 작아진다. L2는 가중치가 0에 수렴하고 L1은 가중치가 0이 될 수 있다고 알고 있다. L1의 경우엔 W가 sparse 해질 가능성이 좀 더 높기 때문에 압축에 용이하다.

이를 Neural Network로 확장하면 다음과 같다. 강의에선 L1은 생략됐다. L2 regularization에서는 Frobenius norm이라는 이름으로 모든 가중치의 제곱을 페널티항으로 사용한다. 그리고 역전파를 위해서 dW도 계산해야 되는데, 이때 Weight decay가 발생한다. 이것 덕분에 가중치가 작게 유지된다.

그래서 정규화가 왜 High Variance 문제를 해결해주는 걸까? Regularization parameter인 lamdba가 커지면 Weigth decay에 의해서 가중치가 감소한다. 가중치가 0에 가까워지는 노드들은 NN에서 없어진다고 생각해도 무방하다. 노드가 몇 개 없어지만 NN의 크기가 감소하기 때문에 Overfitting 문제가 해결된다.
그리고 Activation function으로 tanh를 사용했을 때를 예로 들어서도 설명이 가능하다. W가 감소하면 Z 값도 당연히 감소하게 된다. Z가 작은 구간에서의 tanh는 거의 선형이므로 Variance가 감소하게 된다. 그런데 다른 활성화 함수들을 쓰면 어떻게 되는지에 대한 설명이 부족했다. 그래도 추측해보자면, ReLU나 Leaky ReLU의 경우에는 Z의 절댓값이 작아진다 한들 절댓값이 클 때에 비해서 달라지는 점이 없다. 하지만 얘네는 모든 구간에서 선형이기 때문에 효과가 있지 않을까 싶다.

L2, L1 말고도 Dropout이라는 정규화 방법도 존재한다. 강의에서는 Inverted dropout을 소개한다. 이 방법 말고도 다른 dropout이 뭐가 있나 찾아보니 dropconnect 같은 변형들이 존재하는 것 같다. Dropout은 각 레이어에서 무작위로 노드를 날려버리기 때문에, L2처럼 NN의 크기가 감소해서 Overfitting을 줄일 수 있다. 학습 과정에서 무작위로 사용하지 않을 노드를 결정하기 때문에 각 노드의 가중치도 한쪽으로 편향되지 않는 효과도 있다. (3) 번 과정을 하는 이유는 a의 기댓값을 맞춰주기 위해서다. 이를 생략하면 Test time에 비용이 많이 들게 된다. Test time엔 droptout을 하지 않고 계산한다. Overfitting이 없는 경우에는 이 방법을 적용한다고 좋아지지 않는다. 하지만 컴퓨터 비전 같이 데이터가 부족한 영역에서는 dropout을 잘 사용한다.

정규화 말고도 High Variance 해결 방법은 두 가지가 더 있다. 하나는 Data augmentaion, 다른 하나는 Early stopping이다. 전자는 컴퓨터 비전 등의 영역에서 사진을 뒤집고 돌리고 확대하는 등의 방법으로 원래 있던 데이터를 사용해서 추가적인 데이터를 만드는 방법이다. 물론 완전 독립적인 데이터들에 비해서는 성능이 좋지 않지만, 그래도 추가적인 비용 없이 데이터를 더 많이 만들어 낼 수 있다는 장점이 있다.
후자는 신경망이 Overfitting 되기 전에 학습을 중단하는 방법이다. 앤드류 응 교수님은 이 방법보다는 보통 L2를 더 선호하신다고 하셨다. 신경망을 학습하는 데에는 두 가지 해야 하는 일이 있다. 첫 번째는 Cost function을 최소화하는 것이고, 두 번째는 Overfitting을 피하는 것이다. 이 둘은 서로 완전 다른 일처럼 수행되어야 한다. 하지만 Early Stopping은 Overfitting을 피하기 위해서 학습을 일찍 중단하기 때문에 Train set에 대해서 Cost function이 최소화되지 않는다. 대신 적절한 lambda를 찾기 위해 여러 번 학습을 수행하지 않아도 중간 정도의 W를 찾을 수 있다는 장점이 있다.

데이터의 분포를 맞춰주는 것으로도 학습 속도를 높일 수 있다. 데이터의 feature들 중 분포가 너무 다른 feature가 있는 경우엔 경사 하강법이 빠르게 적용되지 않는다. 그래서 학습 데이터의 평균과 분산을 구해서 noramalizing 해주면 이 문제를 해결할 수 있다. 대신 주의할 점이 학습 데이터를 normalizing 할 때 사용한 평균과 분산을 테스트 데이터에도 똑같이 사용해야 한다. 나는 이걸 데이터를 같은 분포에 가져다 놓는 것이라고 이해했다. 만약 테스트 데이터에서 따로 평균과 분산을 구해서 사용할 경우엔 둘은 다른 분포를 갖게 될 것이다.
학습 속도를 저해하는 또 다른 요인으로 vanishing/exploding gradient 문제가 있다. 가중치가 1보다 큰 경우엔 exploding, 1보다 작은 경우엔 vanishing 문제가 발생한다. 이 문제를 해결하기 위해서는 가중치를 초기화할 때 무지 성으로 하는 게 아니라 가중치의 분산을 1/n이나 2/n 정도로 맞춰주면 된다. Activation function으로 tanh를 사용하는 경우엔 1, ReLU는 2로 설정한다. 이 방법을 Xavier initialization이라고 한다.

이번 주차의 마지막으로 Gradient checking이라는 디버깅 방법도 소개됐다. 이 방법은 경사 하강법에 문제가 있다고 생각될 때 적용하면 된다. 기울기의 추정 값이 실제 기울기 값과 얼마나 다른 지 파악해가면서 문제를 해결해가는 방법이다. 오차가 10의 -7승 정도 되면 좋고 10의 -3승 정도 되면 고민을 조금 해봐야 한다.
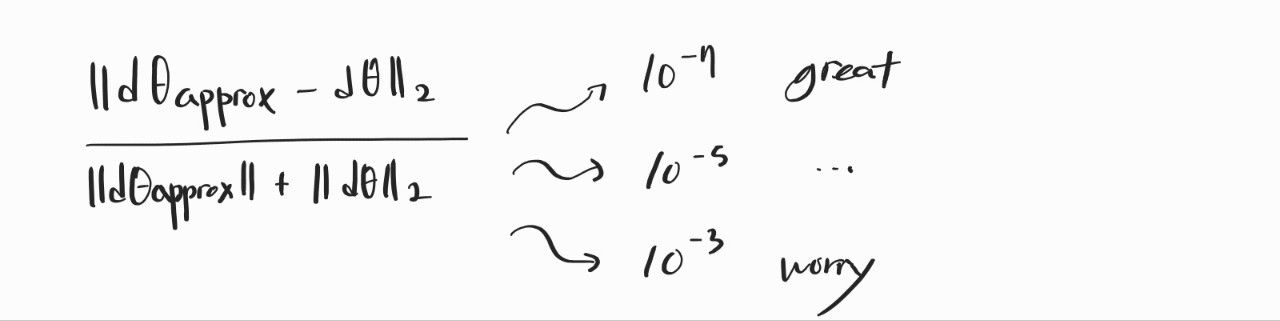
이 방법도 무지성 적용을 하면 안 되는데, 몇 가지 팁이 강의에 언급됐다.
- 학습 중에는 사용하지 말 것. 계산이 너무 오래 걸린다.
- 뭔가 이상한걸 발견했다면, W가 문젠지 b가 문젠지 파악한다.
- Regularization 까먹지 말 것. Gradient에 페널티항을 반영해야 한다.
- Dropout은 사용하지 말 것. Gradient 계산이 복잡해진다.
- W랑 b는 무작위로 초기화하고 조금 학습을 시킨 다음에 grad check를 수행한다.
근데 이 방법을 완전히 이해하지는 못 한 것 같다. 이후에 프로그래밍 과제를 해결하면서 제대로 이해할 수 있기를 바라면서 일단은 넘어갔다.
거의 대부분은 어디선가 한 번쯤은 들어본 키워드들이었지만, 이번 강의는 양이 꽤 됐던 것 같다. 강의 제목이 Practical aspect of Deep Learning이라서 딥러닝을 어떤 분야에 적용하고 어떻게 활용할 수 있는지에 대한 강의일 것 같았는데, 그게 아니라 딥러닝을 구현하는 경우에 실용적인 팁들에 대한 강의였다. 실무를 뛰려면 이 정도 지식은 세포에 새겨져 있어야겠다는 생각이 들었다.
* Courera의 Deep Learning Sepcialization 강의를 수강하는데 도움이 되고자 작성한 요약문입니다. 틀린 내용 있다면 정정해주시면 감사하겠습니다.